INTRODUZIONE

Durante i nostri studi accademici ci siamo scontrati con il problema dell'outlier detection senza però dargli troppa importanza. Questo ci ha portato a raggiungere risultati non ottimali in competizioni di classe e in diversi progetti. Ecco perchè ci siamo proposti di approfondire la tematica e testare dei metodi non supervisionati per l'individuazione di valori anomali. Tali tecniche non solo sono utilizzate per trovare outlier al fine di eliminarli, considerandoli quindi come un noise rispetto alle osservazioni normali, bensì vengono largamente impiegate per unbalanced classification, come poterebbe ad esempio essere la fraud detection.

Ricerca

Dopo una lunga ricerca teorica riguardo a quali tra i molteplici metodi approfondire, abbiamo optato per sei tra questi, ovvero:

• DBSCAN
• OPTICS
• LOF
• kNN
• OCSVM
• ISOLATION FOREST

Di ciascuno di questi metodi potete trovarne un'approfondita descrizione nelle apposite sezioni di questa metodologia.
A questo punto la nostra concentrazione si è spostata sull'individuazione di dataset per outlier detection che contenessero tra le informazioni anche quanti e quali fossero i valori anomali all'interno di ognuno di essi. La nostra ricerca è stata molto fortunata e abbiamo trovato ciò che faceva al caso nostro. Di seguito potete trovare il sito dove sono collezionati i dataset utilizzati nell'analisi: ODDS. C'è però una precisazione da fare riguardo quali dataset sono stati effettivamente da noi utilizzati. Dalla lista riportata sul sito sono stati esclusi i dataset "Yeast", "Seismic", "Heart" e "Mulcross", i primi tre in quanto pur avendo ottenuto i dati non ci è stato possibile ricostruire la variabile identificativa degli outlier, mentre per il rimanente non è più disponibile il dataset. Dalle descrizioni dei dati ci siamo accorti che alcuni tra essi non erano completi, ovvero erano state omesse le variabili qualitative che componevano i dataset. Per quattro è stato possibile recuperare i dataset completi che sono stati aggiunti alla lista dei dati della nostra analisi. Non solo, abbiamo ampliato l'elenco aggiungendo una versione normalizzata dei dataset che già non lo fossero. Nel complesso i dataset sono 53.

Analisi

La nostra analisi è iniziata andando a trasformare le variabili qualitative presenti in alcuni dataset, rendendole binarizzate. Ciò ha portato all'ampliamento del numero di attributi in ogni dataset. Ognuno dei metodi elencati è stato applicato a ciascuno dei 53 dataset, è qui che sono sorti i primi problemi. Ci siamo dovuti confrontare con problemi di tuning dei parametri di alcuni dei metodi, tra i quali il k numero di vicini per DBSCAN, Optics, LOF e kNN e il parametro nu per OCSVM. Soluzioni alle nostre disgrazie vengono presentate dettagliatamente all'interno della descrizione di ogni metodo.
Altro problema fondamentale riscontrato è stato come rendere il più automatizzato possibile trovare il valore soglia oltre il quale considerare le osservazioni outlier. Abbiamo così sviluppato due alternative funzioni di split che sono da ausilio alla nostra decisione. Esse prendono come input i valori degli outlier-score forniti dai diversi metodi ed il numero di osservazioni del dataset in analisi e tramite l'implementazione di tre diversi alberi decisionali, i quali assumono rispettivamente valore di maxdepth pari a 1, 2, 3, forniscono un set di possibili proposte per il valore della soglia. Ciò avviene andando a regredire il numero di istanze (vettore da 1 a n) sullo score, riuscendo in questo modo a trovare regole che dividono lo spazio. Questi possibili split risultano non soggettivi, ma necessitano comunque di una supervisione da parte dell'utente al fine di trovare il miglior valore, anche in caso in cui i valori proposti non siano sensati. Quando accade che i valori soglia delle funzioni split non siano adeguati ai dati in analisi, si decide di porre questo valore pari ad un numero sensato scelto manualmente. Il valore finale viene selezionato tramite visualizzazione grafica degli score in ordine crescente ai quali vengono aggiunti i possibili tagli forniti dalle funzioni. A questo punto si prende il valore soglia che divide due gruppi di osservazioni tra i quali si trova un distaccamento oppure con la cosidetta "regola del ginocchio", cioè quando si nota un'impennata nei valori assunti dallo score.
Il motivo che ci ha portato a creare due funzioni per lo stesso scopo è stato il differente algoritmo utilizzato per produrre l'albero, difatti si contrappongono un Decision Tree ad un Conditional Inference Tree. Una volta scelta la soglia, i valori con score superiori ad essa sono classificati come outlier. Questa classificazione viene salvata in un vettore che ci permette la costruzione di una Confusion Matrix dalla quale ricaviamo le metriche con cui valutiamo i nostri metodi.
Gli indici da noi utilizzati sono stati: AUC (Area Under the ROC Curve), precision e recall.

Per i metodi per i quali sono state implementati più versioni in base ai diversi parametri, sono state riportate le performance migliori. Non sempre è stato chiaro quale implementazione del modello scegliere perchè ad un aumento di AUC spesso corrispondeva una diminuzione di precision, a volte anche drastica. Abbiamo deciso di privilegiare il conseguimento di un AUC più alto, ma in situazioni di grandi cambiamenti degli indici tra le versioni, abbiamo selezionato il modello con il miglior bilanciamento tra i valori, anche se a discapito di qualche punto percentuale in meno sull'AUC.
Nelle conclusioni è possibile trovare la tabella riassuntiva dei risultati per ogni metodo su ogni dataset.

Cluster Analysis sui risultati

Al fine di ottenere un'aggregazione ed una migliore interpretazione dei nostri risultati abbiamo deciso di analizzare la composizione dei dataset e farne una cluster analysis. In questo modo siamo riusciti ad ottenere un raggruppamento tra dataset la cui caratteristica discriminante si è rivelata essere il numero di osservazioni (n), come ci aspettavamo.
Dei 5 cluster ottenuti abbiamo voluto mettere in luce le performance dei diversi metodi e mostrarne punti di forza e criticità.
Al fine di mostrare l'andamento complessivo di ogni metodo abbiamo creato dei grafici che mostrassero l'AUC ottenuto nei diversi dataset con p ed n.

DBSCAN

Il DBSCAN (Density-Based Spatial Clustering of Applications with Noise) è un algoritmo di clustering density based che si basa su tre concetti fondamentali: Core, Border e Noise.
Le osservazioni del dataset vengono classificate in queste tre categorie in base al numero di osservazioni che stanno dentro una sfera multidimensionale con centro nell’osservazione stessa. I due parametri che definiscono il DBSCAN sono EPS e MinPts, che agiscono nella seguente maniera.
EPS misura il raggio da assegnare alla sfera, mentre MinPts stabilisce il numero minimo di punti che devono essere all’interno della sfera per poter considerare l’osservazione in questione come Core. I punti di Core sono, come definito, le osservazioni che soddisfano questa condizione, mentre si definiscono punti di Border le osservazioni che sono all’interno della sfera multidimensionale di almeno un punto di Core, ma non soddisfano la condizione per essere considerati Core. I punti di Noise sono semplicemente le osservazioni restanti, ovvero quelle che non entrano mai nel raggio di un punto di Core.
Questo metodo garantisce che i punti di Core siano sempre nello stesso cluster finale, mentre non è robusto per quanto riguarda le osservazioni Border.
I vantaggi di questo metodo sono evidenti: data la sua semplicità è poco oneroso computazionalmente e può quindi essere applicato anche su dataset enormi nei quali metodi concorrenti più complessi risultano troppo pesanti. Risulta anche robusto rispetto a problemi riscontrabili in cluster analysis tradizionali.
Presenta anche delle criticità non trascurabili: la sua semplicità lo rende eccessivamente rigido e in grado di identificare solamente cluster della medesima densità ed è inoltre fortemente dipendente dalla scelta dei parametri Eps e MinPts.
Si è dimostrato altresì sostanzialmente inutile su dati con un numero rilevante di variabile qualitative in classi. DBSCAN ha ottenuto risultati operativi ottimali con dataset di dimensioni ridotti, mentre è risultato poco efficace su dataset con numero di attributi particolarmente alto.
Nella nostra analisi abbiamo deciso di porre il numero MinPts pari al valor medio tra il logaritmo del numero di osservazioni, numero di attributi più 1 e 2 volte il numero di attributi. Con tale media ci si è assicurati che MinPts sia maggiore del numero di colonne, condizione posta dai creatori del package R DBSCAN. Grazie all’inserimento del logaritmo del numero di osservazioni nella formula si riesce a dare un peso alla dimensione osservazionale del dataset. Per trovare il valore di EPS, secondo parametro del metodo, abbiamo ordinato in senso crescente tutte le distanze risultanti da un KNN con numero di neighborood pari a MinPts trovato al passo precedente. Abbiamo utilizzato le funzioni di split per avere delle proposte di taglio. Una volta presa la decisione su Eps il DBSCAN identifica le osservazioni Outlier classificandoli come punti di Noise.

OPTICS

L’OPTICS (Ordering points to identify the clustering structure) è un algoritmo di clustering density-based che si basa sulla medesima logica del DBSCAN, ma riesce a superare la criticità principale di quest’ultimo, l’incapacità di riconoscere cluster di diverse dimensioni, tramite un meccanismo di discesa del gradiente.
Il valore settato di epsilon è opzionale e ha solamente funzione di migliorarne l’efficienza computazionale. Esso è generalmente molto maggiore rispetto alla EPS del DBSCAN in quanto funge solamente da limite massimo.
Nella nostra analisi si è deciso di porre il numero MinPts pari al valor medio tra il logaritmo del numero di osservazioni, numero di attributi più 1 e 2 volte il numero di attributi. Tale metodo non è più dipendente dalle distanze in quanto tali ma delimita e riconosce come concluso un dataset quando la differenza, in termini di distanze, tra l’osservazione già all’interno e quella successiva risulta troppo elevata.
Il metodo Optics originario, sia con Extract-Xi (discesa del gradiente) che tramite Extract DBSCAN (che si riconduce ad un DBSCAN standard), non sono adeguati all’obbiettivo di Outlier Detection. Pertanto si è utilizzata una variante: OPTICS-OF (outlier factor), che è adeguato allo scopo. Il presupposto di partenza di un'analisi di Outlier Detection tramite OPTICS-OF è che essere outlier non è una condizione binaria, è bensì una proprietà che si applica a tutti i punti appartenenti al dataset con una certa intensità.
Punti cardine sono i concetti di: Core-Distance e Reachability-Distance.

• Core-Distance: di un punto p è la distanza minima epsilon per cui il punto p possa essere definito un punto di Core rispetto ad epsilon e MinPts, tale distanza può risultare non definita quando non esiste un eps tale per cui p si possa definire punto di Core.
• Reachability-Distance: di p rispetto ad o è invece è la misura di distanza minima tale per cui p sia direttamente density reachable da o, se o è un punto di Core nell’ε-vicinato di p. Tale distanza non può mai essere inferiore alla Core-Distance e risulta indefinita qualora non sia un punto di Core.

Sulla base di tali distanze si può calcolare la Local Reachability Distance tramite la seguente formula:
La Local Reachability Distance è quindi l’inverso della media delle reachability distance dei MinPts più vicini. Per questa definizione è necessario che tutte le Reachability distance siano definite, pertanto bisogna settare un numero adeguatamente alto di epsilon. Questa misura è però solamente di appoggio in quanto l’obbiettivo è calcolare, tramite essa, un Outlier Factor da associare a tutte le osservazioni mediante la seguente formula:
Calcolato tale OF, è possibile ordinarlo e visualizzarlo graficamente. Sono state utilizzate le funzioni di split per avere delle proposte di taglio. Una volta presa la decisione sulla soglia, tutte le osservazioni con un OF superiore alla soglia sono state considerate outlier.
Questo metodo operativamente ha ottenuto risultati mediocri, risultando poco performante rispetto agli altri 5 metodi in esame. Raggiunge score minori rispetto al DBSCAN, dal quale deriva, in buona parte dei dataset analizzati.
Migliora le prestazioni se lanciato su dataset normalizzati mentre fatica a gestire dati factor binarizzati. Risulta essere il metodo maggiormente performate su due dataset (Ecoli e Glass N) normalizzati, di dimensioni ridotti e con un outlier rate basso, validandosi come metodo candidato per dataset che condividono tali caratteristiche. Data la necessità di ottenere una Core-distance per tutti i punti appartenenti al dataset, è necessario settare un valore iniziale di Eps molto grande; questo si ripercuote sull’onerosità computazionale del metodo, rendendolo pesante per dataset di dimensioni elevate.
Esiste anche un problema di fallimento di questo metodo in presenza di dati ripetuti: quando all’interno del dataset sono presenti un numero maggiore di MinPts di osservazioni con i medesimi valori per ogni variabile la distanza (Reachability Distance) risultante è pari a 0. Dato che questo zero compare al denominatore in calcoli successivi si genera un Inf che dà luogo ad un errore. Per risolvere questa criticità si è deciso di sovrascrivere ai valori zero un valore molto piccolo, che mantenga l’informazione di una distanza molto ridotto ma che possa essere successivamente utilizzato senza generare problemi: si è scelto la metà del valore minimo delle reachability distance che hanno valore positivo.

LOF

Il LOF (Local Outlier Factor) è un metodo density-based che assegna ad ogni osservazione nel dataset la propensione di quel valore ad essere outlier. Il metodo funziona costruendo dei cluster a densità simile, considerando un numero di nearest-neighbour fissato (MinPts). Le osservazioni nello stesso cluster avranno valore 1. Il MinPts permette di determinare una densità soglia per l’algoritmo di cluster. La densità dei cluster è però dinamica, infatti cluster diversi possono avere densità differenti. Questa proprietà supera le criticità del DBSCAN nel riconoscimento di cluster tutti a medesima densità.
Il LOF di un oggetto p è:

Dove lrd (local reachability density) è l'inverso della distanza di raggiungibilità media basata sui vicini MinPts (vedi formula in OPTICS).
E’ interessante come questo metodo sia in grado di gestire bene dati con molti attributi ed in particolar modo se presenti molte variabili qualitative in classi.
Nella nostra analisi abbiamo deciso di porre il numero MinPts (corrispondente al k del metodo kNN) pari al valor medio tra il logaritmo del numero di osservazioni, numero di attributi più 1 e 2 volte il numero di attributi. Dopo aver calcolato gli score del LOF li abbiamo ordinati in ordine crescente e abbiamo utilizzato le funzioni di split per avere delle proposte di taglio. Una volta presa la decisione sulla soglia, tutte le osservazioni con un outlier factor superiore alla soglia sono state considerate outlier.
Come ci si aspettava dalla teoria, questa metodologia non è stata efficiente per dataset ad alta dimensionalità in quanto produce vettori molto grandi in termini di memoria che non sono allocabili e utilizzabili nell'analisi. Risulta, quindi, fallimentare l'utilizzo del LOF nei dataset come "Shuttle", "Http", "ForestCover" e "Smtp".

kNN

L’algoritmo di outlier detection basato sul metodo k-Nearest Neighbour è un algoritmo distance based estremamente semplice: una volta settato il numero k di nearest neighbour, si va a calcolare la distanza tra ogni osservazione e i suoi k vicini. Dopo aver ottenuto le k misure di distanze si va a calcolarne una media, questa distanza media rappresenta proprio l’outlier score di ogni osservazione.
Questo modo di procedere si basa sul concetto banale che osservazioni più lontane sono più diverse tra loro, quindi osservazioni outlier, diverse da tutte le osservazioni normali del dataset, risulteranno perciò avere una distanza maggiore.
Sebbene concettualmente molto semplice, abbiamo riscontrato diverse difficoltà. In primo luogo il tuning del parametro k. Mentre in caso di classificazione o regressione è sufficiente implementare una cross-validation per trovare il numero di vicini ottimale, per riuscire ad ottenere previsioni accurate, nel caso dell’outlier detection questo non è possibile, in particolare, per come abbiamo deciso di strutturare l’analisi con metodi unsupervised, non abbiamo a nostra disposizione una variabile risposta.
Abbiamo pensato di selezionare casualmente delle variabili del nostro dataset utilizzandole come variabili risposta per fittare una regressione e calcolare il k ottimale, tuttavia abbiamo scartato questo metodo, non solo per pesantezza computazionale ma anche perché lo scopo della nostra analisi è diverso da quello di una previsione accurata rispetto ai vicini.
Cercando in letteratura non sono emerse molte indicazioni su come settare questo parametro in modo ottimale, quindi, appoggiandoci anche alla teoria trovata per il DBSCAN, abbiamo deciso di provare delle misure di sintesi basate sul numero di righe e sul numero di attributi: abbiamo implementato tre kNN diversi con k= min(log(n), p+1), k=max(log(n), p+1) e k=mean(log(n), p+1), in un caso non è stato possibile computare il massimo in quanto eccedeva il numero di variabili, abbiamo allora scelto di utilizzare (n-1). Dai dati analizzati, purtroppo non sembra esserci un trend o una motivazione guidante la scelta di k. Questa andrebbe approfondita andando a caratterizzare più a fondo la struttura dei dati, lo consigliamo per un futuro lavoro.
Per cercare di risolvere questo problema abbiamo provato ad utilizzare un algoritmo di kNN aggregato, che va a calcolare le distanze, fornendone poi una media, che vanno da un k minimo, settato come min(log(n), p+1), e un k massimo, settato come max(log(n), p+1).
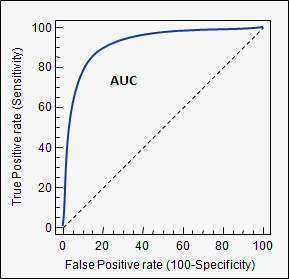
Questa tecnica non si discosta particolarmente dall’altra in termini di AUC e circa nel 17% dei casi siamo riusciti ad ottenere performance migliori con l'aggregazione.
Il secondo problema che siamo stati chiamati ad affrontare è dovuto alla complessità computazionale dovuto al calcolo delle distanze, questo è stato agevolmente risolto attraverso l’utilizzo di un algoritmo kNN-kdTree, questa tecnica utilizza un kd-Tree per suddividere lo spazio delle osservazioni andando a ristrutturare l’intero dataset in un albero. Per ogni osservazione che si intende analizzare si scorre l’albero fino a trovare la regione di spazio dove è allocato questo punto e qui, viene calcolata la distanza con i vicini situati nella stessa regione. Riducendo la complessità computazionale sia in termini di tempo che di memoria.
La funzione usata permette diversi tipi di ricerca, quello da noi utilizzato è sempre stato il searchtype standard. Inoltre è possibile, se lo si desidera andare a calcolare Approximate kNN, tecnica non utilizzata da noi che potrebbe però risultare vincenti in dataset ad elevate dimensioni.
Per quanto riguarda l'assegnazione della classe (outlier o no) alle osservazioni si sono utilizzate le funzioni di split, come per i metodi sopra descritti. Una considerazione finale che possiamo fare è che le performance del kNN, sono risultate migliori in dataset non scalati rispetto a dataset scalati, ciò invece si inverte di tendenza quando nel dataset andiamo ad aggiungere variabili dicotomiche, quello che si è potuto osservare nei quattro casi di dataset a cui è stata aggiunta una versione completa, è stato un miglioramento dei risultati nel caso normalizzato (che rimane comunque inferiore di quelli ottenuti prima dell'aggiunta di varibili binarie). Questo probabilmente dovuto al fatto che scalando i suddetti vengano compressi andando a mascherare le distanze elevate. Nel complesso possiamo affermare di avere ottenuto risultati buoni con questo metodo.

OCSVM

L’algoritmo Support Vector Machine (SVM) è un metodo basato su due classi, la classe negativa e la classe positiva {-1,1}. Una proprietà molto utile di questa tecnica, è la creazione di decision boundary che possono anche essere non lineari proiettando, quindi, i dati con funzioni non lineari su spazi a grandi dimensioni. Si separano in questo modo le osservazioni sull’iperpiano tramite appunto una linea di decision boundary con un margine nu; nu è il limite superiore della frazione dei margini di errore e il limite inferiore della frazione di vettori di supporto.
Dunque la scelta di nu è molto importante perché determina l’ampiezza di banda che andremo a scegliere e quindi anche quante osservazioni vengono lasciate a destra o sinistra di essa. I vettori di supporto sono quei punti (o dati) che delineano la banda che va a crearsi e sono trovati cercando la decision boundary che massimizza la distanza tra osservazioni risultanti nelle diverse classi.
La One-Class SVM è un’estensione della metodologia SVM dove si utilizzano solo le informazioni di una classe (per questo si chiama “one-class”), cioè si trasformano le feature attraverso il kernel scelto e si tratta l’origine come il solo membro della seconda classe. Risulta essere una tecnica molto sensibile alla scelta dei parametri. Tra questi si è dovuto scegliere:

• un opportuno kernel: abbiamo scelto il kernel radiale utilizzato nelle classificazioni;
• il valore di gamma: è il numero di parametri liberi in una Gaussian radial basis function, abbiamo scelto di assegnare a gamma valori differenti in base alla funzione da noi utilizzata;
• nu: già spiegato in precedenza.

Questo algoritmo funziona bene con rappresentazioni binarie (difatti raggiunge AUC più alti sui dati scalati), inoltre dipende dal numero di features in analisi (con 10 feature funziona bene il kernel radiale), ma aumentando il numero di feature diminuiscono di molto le performance.
Nella nostra analisi abbiamo deciso di implementare sei diverse OCSVM. Quattro con la funzione base di R nelle quali si utilizza un kernel radiale, gamma è stato settato con il valore di default, cioè 1/(numero di osservazioni) e nu invece può assumere i valori 0.01, 0.1, 0.5 (valore di default) e 0.9 . E’ emerso che per dataset grandi funziona meglio nu settato con valore di default e in caso di dataset con strutture complesse dove è difficile la determinazione di valori anomali spesso è opportuno settare nu con 0.1.
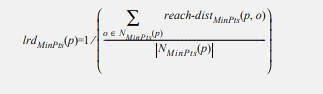
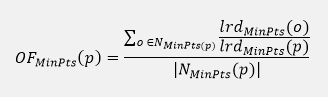
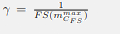
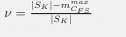Altre due OCSVM invece sono state implementate seguendo le indicazioni riportate su un paper di riferimento dove si sfruttano le distanze con kNN e si calcolano le derivate dell’approssimazione del vettore delle distanze medie attraverso una funzione continua per ricostruire i valori dei parametri nu e gamma. In particolare, i valori di gamma e nu sono: , dove FS è la funzione approssimata e .
Il paper consiglia un k uguale a 7 come numero di nearest-neighbourn, ma noi abbiamo voluto testare anche k pari al numero ottimale di vicini trovato attraverso il metodo kNN, precedentemente presentato, che ha raggiunto un AUC più alto.
Si sono riscontrati alcuni problemi nel calcolo del valore del parametro nu perché spesso per dataset grandi esso non stava nel range prefissato (0,1), ma poteva assumere valori molto grandi anche in negativo. In questi casi abbiamo deciso di procedere lasciando nu col suo valore di default.
Questa tecnica funziona bene con k=7 soprattutto per dataset grandi e con dati normalizzati, dove consente di ottenere buoni risultati rispetto ad altri metodi. Si è osservato che se il numero k trovato attraverso kNN risultasse molto grande allora in questo caso, il miglior k da settare è risultato essere quest’ultimo. Si può dire in generale che la OCSVM è un metodo che consente di ottenere performance sufficienti anche quando tutti gli altri metodi performano male, ma con dataset non scalati e con dati molto sparsi non riesce ad essere ottimizzato e non produce risultati ottimali come gli altri metodi (vedi dataset Musk).

ISOLATION FOREST

L’isolation Forest (IF) è una tecnica innovativa di outlier detection. Questo algoritmo è costruito appositamente per trovare anomalie nei dati, quindi a differenza di altri, non si concentra sulla classe normale per poi trovare la classe minoritaria, ovvero gli outlier, ma si focalizza sull’individuazione di osservazioni anomale.
Per riuscire in tale individuazione si parte dalle proprietà quantitative degli outlier: questi sono poche osservazioni e i valori dei loro attributi sono molto differenti dalle osservazioni normali.
Data questa diversità di attributi si immagina che le osservazioni anomale siano più facili da isolare, questo vuol dire che immaginando la costruzione di un albero che divida lo spazio delle osservazioni e delle variabili, un valore anomalo andrà a posizionarsi verso la radice dell’albero, proprio per la sua attitudine ad essere facilmente separato, al contrario, osservazioni normali, essendo più difficili da separare tra di loro, si troveranno ad una profondità più elevata. E’ proprio su questo semplice concetto che si basa l’algoritmo, chiamiamo questo albero Isolation Tree (iTree).
L’Isolation Forest (iForest) non è altro che un ensemble di Isolation Tree. Costruito questo ensemble model, le anomalie sono quelle osservazioni che hanno un path in media corto negli iTree, ovvero l’osservazione si trova in media più vicina alla radice.
Per implementare un iTree l'utente è tenuto a scegliere il sample size delle osservazioni totali su cui costruire gli alberi. L’albero costruito è completo, ovvero ogni foglia contiene una sola osservazione, la profondità massima con cui viene costruito l’albero arriva alla lunghezza media del path. La dimensione del sample non deve essere elevata, infatti gli Isolation Tree funzionano meglio con un campione ridotto, si è osservato empiricamente che anche con grandi dataset un campione di 256 osservazioni è sufficiente, questo perché con campioni piccoli si è in grado di evitare i fenomeni di swamping e masking:

• swaping: è il fatto di identificare erratamente osservazioni normali come anomalie;
• masking: è il fatto di non riuscire a separare in modo efficiente gli outlier se si trovano in piccoli cluster molto densi.

In ogni albero l’insieme di osservazioni del campione viene divisa ricorsivamente selezionando in modo casuale uno degli attributi e il valore di split.
Nell’Isolation Forest il numero di alberi desiderato va settato dall’utente, è stato osservato empiricamente che si ottiene una convergenza della lunghezza del path già con 100 alberi, tuttavia essendo un metodo tendenzialmente rapido, la complessità computazionale è bassa, quindi, possono essere settati senza problemi anche più alberi. Per valutare le anomalie si definisce la lunghezza di path, h(x), di ogni punto x che è misurata tramite il numero di nodi che l’osservazione x attraversa in un Isolation Tree dalla radice al nodo terminale in cui questa di trova. Dato un dataset di n istanze, la definizione di average path data nella sezione 10.3.3 di B. R. Preiss. Data Structures and Algorithms with Object- Oriented Design Patterns in Java. Wiley, 1999.
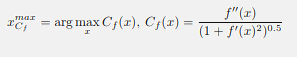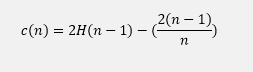Risulta essere: dove H(i) è il numero armonico che può essere calcolato come ln(i)+0.5772156649 (costante di Eulero). Dato che c(n) è la media di di h(x) dato n, viene usata per normalizzare h(x).
L’anomaly score di un’osservazione viene calcolata come: dove E(h(x)) è il valore atteso degli h(x) in ogni iTree.
Se l’osservazione ha uno score vicino ad 1 allora è quasi certamente un outlier, se, al contrario, l’osservazione ha uno score molto minore di 0.5, allora è da considerarsi come osservazione normale. Inoltre, se tutte le istanze hanno uno score che è circa 0.5 allora l’intero campione non contiene nessuna distinta anomalia. E' necessario decidere uno split per identificare la soglia oltre la quale le osservazioni con quello score sono considerate anomale, ciò avviene con l'ausilio delle nostre funzioni di split.
Possiamo inoltre fare delle considerazioni aggiuntive; data la natura di campionamento delle osservazioni, ma anche delle variabili, questo metodo riesce generalmente a performare bene su dataset con un grande numero di istanze e quando si trattano dataset con molte dimensioni dove sono presenti attributi irrilevanti.
Nella nostra analisi, possiamo infatti notare come l’IF abbia raggiunto ottimi risultati in dataset con un elevato numero di righe, dove la maggior parte degli altri metodi ha invece fallito. Non possiamo valutare in modo significativo l’affermazione dell’efficienza dell’algoritmo su dataset con un numero di attributi p molto grande, in quanto l’unico dataset con tali caratteristiche "Speech", non ha prodotto risultati soddisfacenti per nessuno dei metodi utilizzati, possiamo pensare che questo sia dovuto alla struttura stessa dei dati.
Un’ulteriore osservazione che possiamo fare osservando i risultati ottenuti nella nostra analisi, è che l’IF ottiene generalmente risultati peggiori quando i dati vengono scalati rispetto ai dati in scala originale,anche in caso di inserimento di variabili factor all'interno del dataset.
In conclusione possiamo dire che le caratteristiche uniche che contraddistinguono un outlier permettono all’iForest di costruire modelli parziali (come detto prima gli alberi non vengono costruiti interamente) e utilizzare solo una piccola porzione di dati di training per costruire modelli efficienti. Come risultato l’algoritmo non è oneroso a livello di tempo e a livello computazionale e richiede l’impiego di poca memoria, il che rende il metodo ideale per dataset grandi.

CONCLUSIONI

Viene di seguito riportata la tabella con i risultati complessivi dell'analisi svolta.

BIBLIOGRAFIA

[1] Breunig, M. M., Kriegel, H. P., Ng, R. T., & Sander, J. (2000, May). LOF: identifying density-based local outliers. In ACM sigmod record (Vol. 29, No. 2, pp. 93-104). ACM.

[2] Schölkopf, Bernhard, et al. "Support vector method for novelty detection." Advances in neural information processing systems. 2000.

[3]Bennett, Kristin P., and Erin J. Bredensteiner. "Duality and geometry in SVM classifiers." ICML. 2000.

[4]Friedman, Jerome, Trevor Hastie, and Robert Tibshirani. The elements of statistical learning. Vol. 1. No. 10. New York, NY, USA:: Springer series in statistics, 2001.

[5] Liu, Fei Tony, Kai Ming Ting, and Zhi-Hua Zhou. "Isolation forest." 2008 Eighth IEEE International Conference on Data Mining. IEEE, 2008..

[6]Manevitz, Larry M., and Malik Yousef. "One-class SVMs for document classification." Journal of machine Learning research 2.Dec (2001): 139-154.

[7] Schubert, Erich, et al. "DBSCAN revisited, revisited: why and how you should (still) use DBSCAN." ACM Transactions on Database Systems (TODS) 42.3 (2017): 19.

[8] Sander, Jörg, et al. "Density-based clustering in spatial databases: The algorithm gdbscan and its applications." Data mining and knowledge discovery 2.2 (1998): 169-194.

[9] Chang, Chih-Chung, and Chih-Jen Lin. "Training v-support vector classifiers: theory and algorithms." Neural computation 13.9 (2001): 2119-2147.

[10] Ghafoori, Zahra, et al. "Unsupervised parameter estimation for one-class support vector machines." Pacific-Asia Conference on Knowledge Discovery and Data Mining. Springer, Cham, 2016.

[11] Breunig, Markus M., et al. "Optics-of: Identifying local outliers." European Conference on Principles of Data Mining and Knowledge Discovery. Springer, Berlin, Heidelberg, 1999.

[12]MKriegel, Hans-Peter, Peer Kröger, and Arthur Zimek. "Outlier detection techniques." Tutorial at KDD 10 (2010).

[13]Upadhyaya, Shuchita, and Karanjit Singh. "Nearest neighbour based outlier detection techniques." International Journal of Computer Trends and Technology 3.2 (2012): 299-303.

[14]Ismo, K. "Outlier detection using k-nearest neighbour graph." null. IEEE, 2004.

[15]Divya, K. T., and N. Senthil Kumaran. "IMPROVED OUTLIER DETECTION USING CLASSIC KNN ALGORITHM." (2016).

[16]Bay, Stephen D., and Mark Schwabacher. "Mining distance-based outliers in near linear time with randomization and a simple pruning rule." Proceedings of the ninth ACM SIGKDD international conference on Knowledge discovery and data mining. ACM, 2003.

[17]Ramaswamy, Sridhar, Rajeev Rastogi, and Kyuseok Shim. "Efficient algorithms for mining outliers from large data sets." ACM Sigmod Record. Vol. 29. No. 2. ACM, 2000.

[18]Orair, Gustavo H., et al. "Distance-based outlier detection: consolidation and renewed bearing." Proceedings of the VLDB Endowment 3.1-2 (2010): 1469-1480.

[19]http://odds.cs.stonybrook.edu/